Deviance (statistics)

In statistics, deviance is a quality of fit statistic for a model that is often used for statistical hypothesis testing.

1 Definition
2 See also
3 Notes
4 References
5 External links

Definition

The deviance for a model M₀, based on a dataset y, is defined as^[1]

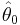$D(y) = -2 [\log \lbrace p(y|\hat \theta_0)\rbrace -\log \lbrace p(y|\hat \theta_s)\rbrace ].\,$

Here $\hat \theta_0$ denotes the fitted values of the parameters in the model M₀, while 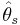$\hat \theta_s$ denotes the fitted parameters for the "full model": both sets of fitted values are implicitly functions of the observations y. Here the full model is a model with a parameter for every observation so that the data are fitted exactly. This expression is simply −2 times the log-likelihood ratio of the reduced model compared to the full model. The deviance is used to compare two models - in particular in the case of generalized linear models where it has a similar role to residual variance from ANOVA in linear models.

Suppose in the framework of the GLM, we have two nested models, M₁ and M₂. In particular, suppose that M₁ contains the parameters in M₂, and k additional parameters. Then, under the null hypothesis that M₂ is the true model, the difference between the deviances for the two models follows an approximate chi-squared distribution with k-degrees of freedom.^[1]

Some usage of the term "deviance" can be confusing. According to Collett:^[2]

"the quantity 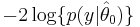$-2 \log \lbrace p(y|\hat \theta_0)\rbrace$ is sometimes referred to as a deviance. This is [...] inappropriate, since unlike the deviance used in the context of generalized linear modelling, 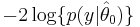$-2 \log \lbrace p(y|\hat \theta_0)\rbrace$ does not measure deviation from a model that is a perfect fit to the data."

Notes

^ ^a ^b McCullagh and Nelder (1989)
^ Collett (2003)

References

McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Chapman & Hall/CRC. ISBN 0412317605.

Collett, David (2003). Modelling Survival Data in Medical Research, Second Edition. Chapman & Hall/CRC. ISBN 1-58488-325-1.

External links

Generalized Linear Models - Edward F. Connor

Lectures notes on Deviance

Statistics

Descriptive statistics

Continuous data

Location	Mean (Arithmetic, Geometric, Harmonic) Median Mode

Dispersion	Range Standard deviation Coefficient of variation Percentile Interquartile range

Shape	Variance Skewness Kurtosis Moments L-moments

Count data

Index of dispersion

Summary tables

Dependence

Statistical graphics

Data collection

Designing studies	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling Stratified sampling Opinion poll Questionnaire

Controlled experiment	Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design

Uncontrolled studies	Natural experiment Quasi-experiment Observational study

Statistical inference

Statistical theory	Sampling distribution Sufficient statistic Meta-analysis

Bayesian inference	Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator

Frequentist inference	Confidence interval Hypothesis testing Likelihood-ratio

Specific tests	Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test

General estimation	Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation

Correlation and regression analysis

Correlation	Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust

Generalized linear model	Exponential families Logistic (Bernoulli) Binomial Poisson

Partition of variance	Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical, multivariate, time-series, or survival analysis

Categorical data	Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test

Multivariate statistics	Multivariate regression Principal components Factor analysis Cluster analysis Copulas

Time series analysis	Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation

Survival analysis	Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model

Applications

Biostatistics	Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Outline
Index

Least squares and regression analysis

Computational statistics

Least squares · Linear least squares · Non-linear least squares · Iteratively reweighted least squares

Correlation and dependence

Pearson product-moment correlation · Rank correlation (Spearman's rho, Kendall's tau) · Partial correlation · Confounding variable

Regression analysis

Ordinary least squares · Partial least squares · Total least squares · Ridge regression

Regression as a
statistical model

Linear regression	Simple linear regression · Ordinary least squares · Generalized least squares · Weighted least squares · General linear model

Predictor structure	Polynomial regression · Growth curve · Segmented regression · Local regression

Non-standard	Nonlinear regression · Nonparametric · Semiparametric · Robust · Quantile · Isotonic

Non-normal errors	Generalized linear model · Binomial · Poisson · Logistic